The Power of Self-Service Analytics
180
partner institutions6%
retention rate increase using Rapid Insight to target academic support at a large public university99.5%
accuracy predicting incoming class size at a mid-size public universityToo often, access and capacity issues keep staff from using data to make fast and effective decisions. Rapid Insight puts reliable data in decision-makers’ hands with simplified predictive modeling, a code-free data workspace, and cloud-based dashboards. Empower users across your institution—from IR teams to advisors to the registrar’s office—to analyze and quickly act on campus data with Rapid Insight.
Construct a data-informed environment
Rapid Insight’s code-free data ingestion workspace allows you to connect to every source on campus, from your SIS and LMS to your CRMs and databases. Repeatable data workflows automatically cleanse and prepare data, quickly producing reliable reports and trustworthy datasets.
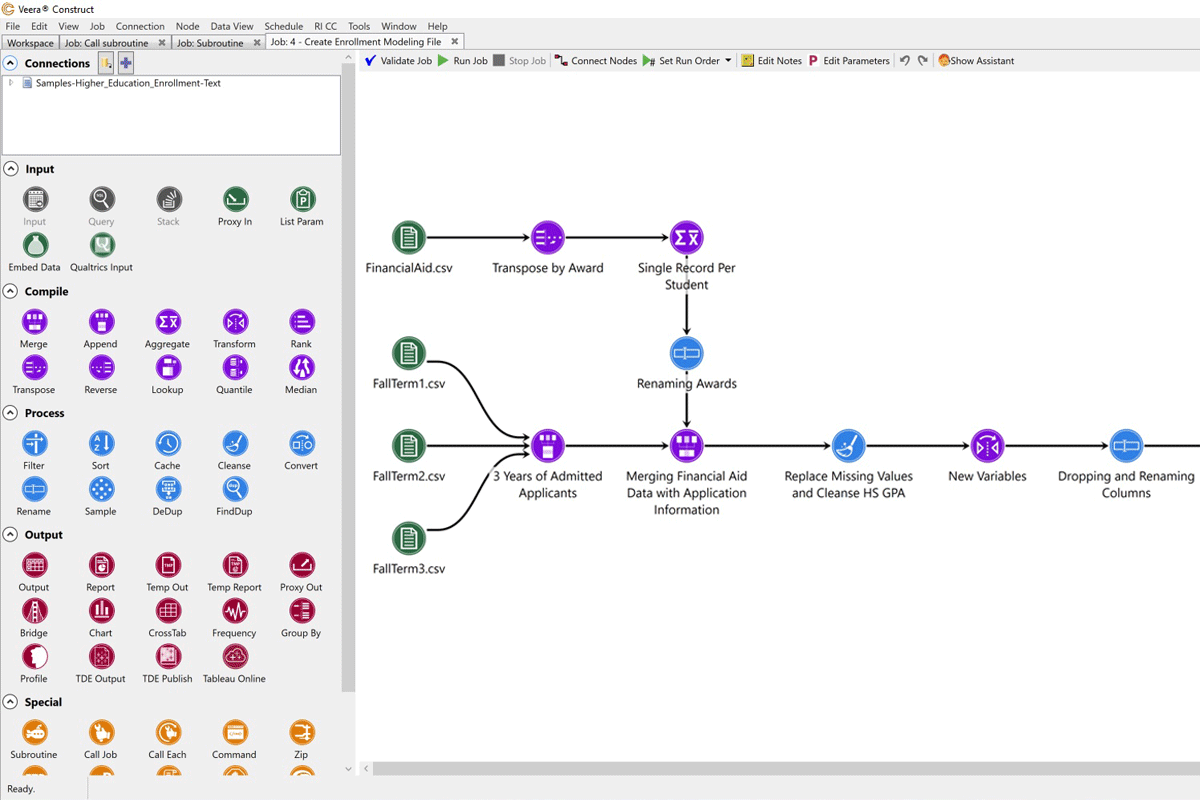
Predict key outcomes
When anyone on campus can build a predictive model with a single click, you can make tactical and timely decisions about enrollment, student support, advancement, and more. Rapid Insight mines your data for the most statistically significant variables and produces an instant model for your analysis.
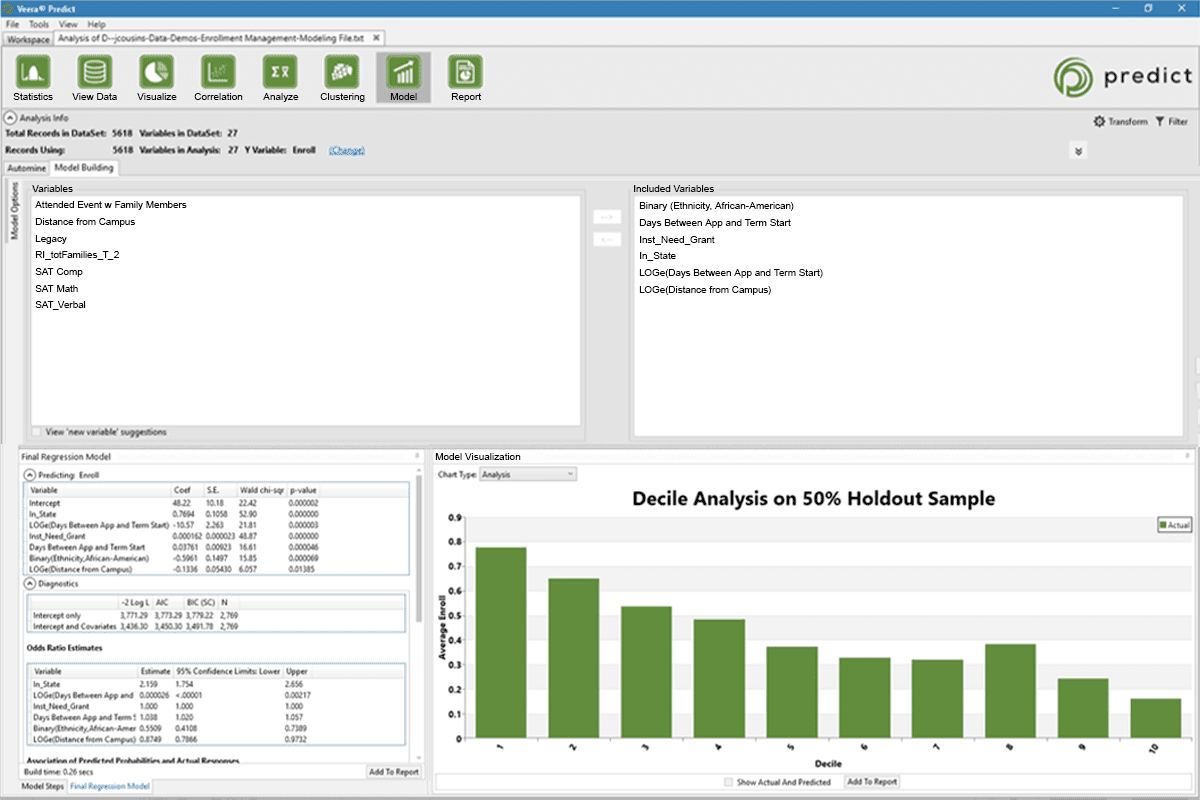
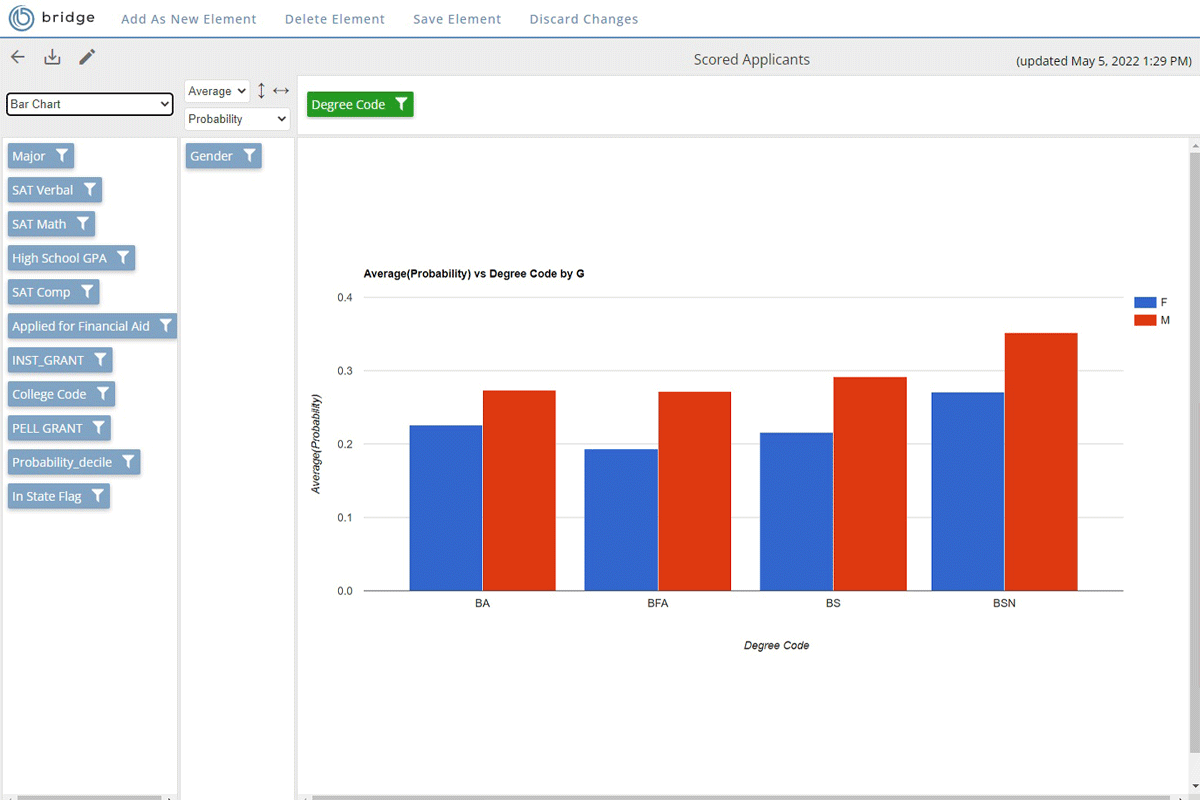
Bridge the gap between insight and action
Rapid Insight’s higher education analytics platform gives your stakeholders the information they need in their ideal format. Cloud-based dashboards open in any internet browser and allow users to customize their view and explore data in-depth. Your organization’s data manager governs which data each user can access.
Learn, troubleshoot, and strategize
Rapid Insight partners enjoy unlimited support from higher education data analytics experts. Access technical assistance, attend regular product trainings, get feedback on models and data workflows you build, and receive strategic guidance on planning and executing data initiatives.
Talk to Our Team
Senior Strategic Leader, Data and Analytics
Specialties Student Success, Annual Giving, Admissions, Data and Analytics, Stakeholder Communication and Enfranchisement, Customer Service, Business Intelligence
Strategic Leader, Data and Analytics
Specialties Student Success, Enrollment Strategy, Data and AnalyticsLevel up your analytics with Rapid Insight
To speak with an expert or request a demo, please submit this form.
Case Study Spotlight
Latest Research and Insights

3 reasons your colleagues don’t want to use data—and how to change their minds
6 steps to build a predictive model

4 reasons to streamline your data reporting
Explore Related Solutions
Edify
Pair powerful data warehousing technology with direct-to-user analytics tools to empower better decision-making across campus
Learn MoreNavigate360
Navigate360 is the CRM trusted by 850 schools to recruit, retain, and empower students in college and beyond
Learn More